城地　茂（台湾・国立高雄第一科技大学）

大衍暦（一行、728年。763年日本伝来）では、８尺の"表" (gnomon)の影長を一覧表にする方法が述べられていた事が、Cullen（1982年）によって再発見された。２次の階差により表示されていたため、当時から余り理解されていなかったのか、『旧唐書』や『新唐書』といった歴史書にも正しく記録されていなかったので、現代の科学史家に知られていなかったのである。これは、インドですでにSIN表が作られていたものの、TAN表としては世界最古のものである。

その後、『大衍暦』とほとんど同じである『宣明暦』（徐昂、822年。861年日本伝来）の朝鮮版本より、当時のTAN表が復元された。

しかし、従来、現代科学史家たちは、全天を365.25に分割する漢代の伝統的"華度"法で再計算し、誤差を計算するなどの研究しか行わなかった。筆者は、逆に、表の数値から、"華度"を求めてみると、

１"華度" ≒ 360/364°

に近いことが分かった。"華度"は、太陽が一日に度（＝渡）る角度を表わすものであるから、漢代にすでに365と1/4とより近い値が出てているにも関わらず、唐代になって、誤差の多い数値を使っているのである。これは、筆者の仮説ではなく、この値を使っていた唐代の暦法からも示される。

全天を364に分割するということは、一象限を91に分割するということで、これは、実際に大きな円の模型を作る上での便宜を考えたものではないかと想像される。南北朝の祖冲之が円周率を計算したときも模型を作ったという記述が残っており、中国の伝統的な手法である。したがって、１"華度"毎の数値を実測して、TAN表を作ったものと考えられ、従来から論争されてきた、インドからの伝来説を否定する一つの証左と言えよう。

１　『大衍暦』、『宣明暦』のＴＡＮ表　　中国では、古来より８尺の”表”（gnomon）を立てて、その影の長さから様々な天文定数の測定を行っていた。計りである”圭”と共に”圭表”と呼ばれたこの機器の機能は、1) 方向を定める機能2) 季節（二十四節気）を知る機能3) 日時計として時刻を知る機能4) 宇宙論（蓋天論）の構築、測量や太陽までの距離を計る機能の４つと考えられる。　このうちの４番目の機能、太陽までの距離は、「一寸千里」説で説明されていた。つまり、中原地方付近では、南北に１０００里離れた地点で観測すると、８尺の”表”の影は１寸伸縮する。太陽の直下、つまり影の長さが０、までこの「率」で変化するとして、距離を考えていたのである。しかし、唐代になるとこのような素朴な宇宙観は、疑問を持たれた。そして、一行による大規模な観測により否定された。

写真１　一行がいた西安南郊の華厳寺

　この際に、測量地点へ行って、正確に垂直な”表”を立てるということは、技術的に困難だったと思われ、それに代わって太陽の南中高度を測定するという方法が用いられた。そのため角度から影の長さを求める一覧表が必要になったのである。角度は、地表からの高度ではなくて、天頂からの角度でこの表を作ったので、今日のTANの表と全く同じものになった。一行は、そのTAN表を自ら作った『大衍暦』（928年）に記述していたのだが、２階の階差で表示されていたため、当時から余り理解されていなかったのか、『旧唐書』や『新唐書』といった歴史書にも正しく記録されていなかった。このため、現代の科学史家にも知られておらず、1982年になってやっと報告された。

　三角関数については、インドでは古くから研究が進み、５世紀ころには、１象限を２４等分にしたものについてのSINの表ができていた。これは、『開元占経』によって、中国にも伝えられている。しかし、TAN表としては、『大衍暦』の表が世界最古のものである。

　しかし、正確な数値とは思えないような部分も多く、ずっと疑問視されていた。ところが、『高麗史』に記述されている朝鮮版本の『宣明暦』の中に、数値が正確であろうと思われる記述が残っており、復元する事ができた。

　これによれば、TANの表は、以下のように記述されている。

　文章は長いが、同じもので、数値が異なっているだけである。最初の一段落（引用文中の下線部）を訳すと、

　０度と１度の差は、1379で、25度まで、１度増える毎に（差が）１ずつ増加するので、このとき２６増加して（1730になって）いる。

と、いう意味で、以下、数値は異なるが、同様の操作の繰り返しである。これを影の長さそのもので表すと、表１の２行目の数値になる。

　１度と２度では、1379 + 1 = 1380 の差がある。２度と３度では、1380 + 2 = 1382の差になる。つまり、２次の階差が公差１になっている。26度からは公差は２になり、41度からは６になるという意味であった。

表１　『宣明暦』にある１華度毎の表

華度 『宣明暦』 華度 (360/x) 1 .1379 364.5429 2 .2759 364.5188 3 .4141 364.4795 4 .5526 364.4251 5 .6915 364.3556 6 .8309 364.273

7 .9709 364.1764

8 1.1116 364.0686

9 1.2531 363.9498

10 1.3955 363.8209

11 1.5389 363.6849

12 1.6834 363.5419

13 1.8291 363.3939

14 1.9761 363.2428

15 2.1245 363.0897

16 2.2744 362.9387

17 2.4259 362.7896

18 2.5791 362.6456

19 2.7341 362.5086

20 2.891 362.3807

21 3.0499 362.2649

22 3.2109 362.1622

23 3.3741 362.0746

24 3.5396 362.0061

25 3.7075 361.9578

26 3.8779 361.9316

27 4.0509 361.9306

28 4.2267 361.9497

29 4.4055 361.9839

30 4.5875 362.0323

31 4.7729 362.0927

32 4.9619 362.1642

33 5.1547 362.2478

34 5.3515 362.3445

35 5.5525 362.4532

36 5.7579 362.5781

37 5.9679 362.7201

38 6.1827 362.8823

39 6.4025 363.0656

40 6.6275 363.273

41 6.8579 363.5077

42 7.0939 363.7715

43 7.3361 364.0535

44 7.5851 364.3466

45 7.8415 364.6447

46 8.1059 364.9448

47 8.3851 365.0767

48 8.6793 365.0787

49 8.9887 364.985

50 9.3135 364.8269

51 9.6539 364.6326

52 10.0101 364.4261

53 10.3828 364.2227

54 10.7727 364.0334

55 11.1805 363.8692

56 11.6069 363.7433

57 12.0526 363.6658

58 12.5195 363.6285

59 13.0095 363.6295

60 13.5245 363.6678

61 14.0664 363.7463

62 14.6371 363.8682

63 15.2526 363.9105

64 15.9162 363.8984

65 16.6312 363.8551

66 17.4009 363.8058

67 18.2286 363.7745

68 19.1179 363.7836

69 20.0724 363.8501

70 21.0957 363.9931

71 22.1914 364.2287

72 23.3631 364.5681

73 24.6147 365.0233

74 25.9501 365.6014

75 27.3953 366.2449

76 28.9943 366.8794

77 30.8531 367.3285

78 33.1577 367.3688

79 36.1921 366.7988

80 40.3563 365.541

81 46.1843 363.7141

この表は、コンピュータを使えば、簡単に作ることができる。試みに、BASICを作ってプログラムを作ってみると、

DECLARE SUB part (s1, l1, s, d1, d2, d3, chi)PRINT "Yixing's method"OPEN "shadow.txt" FOR OUTPUT AS #1LET pi = 3.1415626#LET chi = (2 * pi) / 365.25LET s = 0LET d1 = .1379LET d2 = .0001part 1, 25, s, d1, d2, .0001, chi

part 26, 40, s, d1, d2, .0002, chi

part 41, 44, s, d1, d2, .0006, chi

part 45, 45, s, d1, d2, .0068, chi

part 46, 50, s, d1, d2, .0002, chi

part 51, 55, s, d1, d2, .0007, chi

part 56, 60, s, d1, d2, .0019, chi

part 61, 61, s, d1, d2, .016, chi

part 62, 65, s, d1, d2, .0033, chi

part 66, 70, s, d1, d2, .0036, chi

part 71, 72, s, d1, d2, .0039, chi

part 73, 73, s, d1, d2, .026, chi

part 74, 74, s, d1, d2, .044, chi

part 75, 75, s, d1, d2, .106, chi

part 76, 76, s, d1, d2, .186, chi

part 77, 77, s, d1, d2, .284, chi

part 78, 78, s, d1, d2, .4, chi

part 79, 79, s, d1, d2, .534, chi

CLOSE

END

SUB part (s1, l1, s, d1, d2, d3, chi)

FOR i = s1 TO l1

LET s = s + d1

LET d1 = d1 + d2

LET d2 = d2 + d3

LET t = 8 * TAN(i * chi)

LET e1 = s - t

LET e2 = e1 / t

REM PRINT #1, USING "## ##.#### ##.#### #.#### #.#### ##.#### ##.#### #.#### #.####"; i; s; d1; d2; d3; t; e1; e2

PRINT #1, i; s; e1; "/"; t; e2

NEXT i

END SUB

　こうして作られた表は、華度（あるいは古度）を360 / 365.25 という漢代の四分暦以来の数値と仮定した場合、56度までは相対誤差が１％以下という正確さである。57度以上になると、１％以下のものもあるが、殆どが１％以上になってしまう。

　しかし、角度が小さい北方、つまり中国の中原地方では、実際の測量では十分有効な値で、このTAN表が使われたことが証明されている。

２　インドのSIN表からの計算。

　従来、TANの表は、インド伝来のSIN表から計算できるのではないか考えられていた。

COS　x = SIN ( 90 - x )であるから、こららの数値から、

TAN x = SIN x / COS x = SIN x / SIN (90 - x)

として、１象限を２４等分したTAN表を作ることは、比較的容易である。

　問題は、ここから、１華度毎の数値を計算する過程である。『宣明暦』で、徐昴は、１華度毎の表から、ある地点の影の長さを計算するときに、線形補間法を使っている。

F(x+h) ≒ F(x) + h * {F(x+1) - F(x)} (x∈ N, x≧1)

例えば、天頂距離10.575華度（陽城、中国河南省登封県の夏至の南中時の角度）なら、

写真２、周公の表と伝えられる石柱。

写真３、陽城にある元代の天文台遺跡。

F(10.575) ≒ F(10) + 0.575 * {F(11) - F(10)} = 1.477955

と、なり、この数値は、『宣明暦』の1.4780に極めて近く、徐昴がこの計算をしたことの

証明である。なお、この方法は、徐昴の独特のものではなく、『周髀算経』以来の中国数学・天文学の伝統的手法である。

　そこで、華度１度毎の計算をするにも、この方法を採ったと考えるのが自然だろう。『開元占経』の表から、１度毎の表を作ると、表４のようになる。

　表２　『開元占経』、巻１０４、推月間量命のSin表

１Ｒ＝３相＝２４段　

Degree 開元占経 3438 Sin x 　誤差

3.75 225 224.8559 .1440582

7.5 449 448.749 .2509766

11.25 671 670.7205 .279541

15 890 889.8199 .1801147

18.75 1105 1105.109 -.1087646

22.5 1315 1315.666 -.6656494

26.25 1520 1520.588 -.5883789

30 1719 1719 1.220703E-04

33.75 1910 1910.05 -5.029297E-02

37.5 2093 2092.922 .078125

41.25 2267 2266.831 .1691895

45 2431 2431.033 -3.295898E-02

48.75 2585 2584.825 .1748047

52.5 2728 2727.549 .4511719

56.25 2859 2858.593 .4074707

60 2978 2977.395 .6047363

63.75 3084 3083.448 .5517578

67.5 3177 3176.298 .7021484

71.25 3256 3255.546 .4543457

75 3321 3320.853 .1469727

78.75 3372 3371.94 6.030273E-02

82.5 3409 3408.587 .4125977

86.25 3431 3430.639 .3608398

90 3438 3438 0

表３　Cullen の方法により作ったTAN表

角度 SIN x / SIN (90 - x) 誤差 誤差 / Tan x

3.75 .06544503 -9.842962E-05 -1.504005E-03

7.5 .1308656 -7.868558E-04 -.0060127

11.25 .1968319 -2.080441E-03 -1.056963E-02

15 .2639383 -4.010886E-03 -.0151963

18.75 .3327311 -6.723136E-03 -2.020591E-02

22.5 .4038698 -1.034376E-02 -2.561162E-02

26.25 .4784388 -1.470664E-02 -3.073882E-02

30 .557393 -1.995724E-02 -3.580462E-02

33.75 .6413701 -2.680856E-02 -.0417989

37.5 .7320741 -3.525281E-02 -.0481547

41.25 .8310117 -4.596472E-02 -5.531176E-02

45 .9404255 -5.957443E-02 -6.334838E-02

48.75 1.063348 -7.693291E-02 -7.234967E-02

52.5 1.203352 -9.987283E-02 -8.299549E-02

56.25 1.365982 -.1306238 -9.562632E-02

60 1.559162 -.1728884 -.1108854

63.75 1.794066 -.2337328 -.130281

67.5 2.090132 -.3240817 -.1550532

71.25 2.476046 -.4698589 -.1897618

75 3.00543 -.72662 -.241769

78.75 3.788764 -1.238574 -.326907

82.5 5.080477 -2.515273 -.495086

86.25 7.641426 -7.615609 -.9966214

表４　線形補間法によって作った１度毎の表

華度 『宣明暦』 360/364 360/365.25 360/364の誤差 360/365.25の誤差

1 .1379 .1380818 .1376093 1.81824E-04 -2.907366E-04

2 .2759 .2761636 .2752185 2.636313E-04 -6.814897E-04

3 .4141 .4142455 .4128278 1.454651E-04 -1.272202E-03

4 .5526 .5523165 .550427 -2.834797E-04 -2.173007E-03

5 .6915 .6903468 .6879849 -1.153171E-03 -3.515065E-03

6 .8309 .8283771 .8255428 -2.522945E-03 -5.357206E-03

7 .9709 .9664074 .9631007 -4.492581E-03 -7.799268E-03

8 1.1116 1.104917 1.101107 -6.682634E-03 -1.049328E-02

9 1.2531 1.244099 1.239812 -9.001017E-03 -.0132879

10 1.3955 1.383281 1.378517 -1.221931E-02 -1.698256E-02

11 1.5389 1.522462 1.517223 -1.643789E-02 -2.167737E-02

12 1.6834 1.663147 1.657333 -2.025282E-02 -2.606738E-02

13 1.8291 1.804734 1.798435 -2.436566E-02 -.0306648

14 1.9761 1.946321 1.939538 -2.977848E-02 -.0365622

15 2.1245 2.087909 2.08064 -3.659129E-02 -4.385972E-02

16 2.2744 2.232461 2.224513 -4.193926E-02 -4.988694E-02

17 2.4259 2.377606 2.369162 -4.829407E-02 -5.673838E-02

18 2.5791 2.522751 2.51381 -5.634856E-02 -6.528974E-02

19 2.7341 2.668103 2.658459 -6.599736E-02 -7.564139E-02

20 2.891 2.818197 2.807924 -7.280254E-02 -8.307576E-02

21 3.0499 2.968292 2.957505 -8.160782E-02 -9.239483E-02

22 3.2109 3.118387 3.107086 -9.251285E-02 -.1038136

23 3.3741 3.270291 3.257907 -.1038086 -.1161928

24 3.5396 3.427624 3.414701 -.1119764 -.1248987

25 3.7075 3.584956 3.571495 -.1225438 -.1360049

26 3.8779 3.742288 3.728289 -.1356115 -.149611

27 4.0509 3.903862 3.888469 -.1470385 -.1624312

28 4.2267 4.070446 4.054483 -.1562533 -.1722164

29 4.4055 4.237031 4.220498 -.168469 -.1850019

30 4.5875 4.403616 4.386513 -.1838841 -.2009873

31 4.7729 4.577266 4.558468 -.1956344 -.2144322

32 4.9619 4.754448 4.735044 -.2074523 -.2268562

33 5.1547 4.931631 4.91162 -.2230692 -.2430797

34 5.3515 5.108813 5.088196 -.2426872 -.2633038

35 5.5525 5.298414 5.275491 -.254086 -.2770085

36 5.7579 5.48979 5.466212 -.2681103 -.2916884

37 5.9679 5.681166 5.656933 -.2867341 -.310967

38 6.1827 5.873989 5.847653 -.3087115 -.3350468

39 6.4025 6.082736 6.054875 -.3197637 -.3476253

40 6.6275 6.291484 6.262908 -.3360162 -.3645921

41 6.8579 6.500231 6.470941 -.3576694 -.3869591

42 7.0939 6.715425 6.682244 -.3784752 -.4116564

43 7.3361 6.946277 6.912305 -.3898234 -.4237952

44 7.5851 7.177127 7.142366 -.4079728 -.4427342

45 7.8415 7.407978 7.372427 -.4335217 -.4690728

46 8.1059 7.653081 7.612252 -.4528184 -.4936476

47 8.3851 7.912435 7.870718 -.4726653 -.5143819

48 8.6793 8.171788 8.129185 -.5075121 -.5501156

49 8.9887 8.431143 8.38765 -.5575571 -.6010494

50 9.3135 8.716024 8.665478 -.597476 -.6480227

51 9.6539 9.011417 8.95986 -.6424828 -.6940403

52 10.0101 9.306809 9.254242 -.7032909 -.7558584

53 10.3828 9.602203 9.548624 -.7805967 -.8341761

54 10.7727 9.941356 9.877944 -.8313446 -.8947563

55 11.1805 10.28448 10.2199 -.8960152 -.9606009

56 11.6069 10.62762 10.56186 -.9792843 -1.045045

57 12.0526 10.9788 10.90381 -1.073796 -1.148789

58 12.5195 11.38639 11.30549 -1.133107 -1.214011

59 13.0095 11.79398 11.71168 -1.215516 -1.297816

60 13.0095 12.20157 12.11788 -.8079271 -.8916216

61 13.5245 12.6385 12.53504 -.8859949 -.9894609

62 14.0664 13.13413 13.02896 -.9322729 -1.037436

63 14.6371 13.62975 13.52289 -1.007351 -1.11421

64 15.2526 14.12537 14.01682 -1.127229 -1.235785

65 15.9162 14.69089 14.55194 -1.225309 -1.364264

66 16.6312 15.31556 15.17446 -1.315644 -1.456738

67 17.4009 15.94022 15.79699 -1.460681 -1.603909

68 18.2286 16.56489 16.41952 -1.663713 -1.809082

69 19.1179 17.33173 17.13946 -1.786169 -1.978441

70 20.0724 18.14596 17.95091 -1.926435 -2.12149

71 21.0957 18.9602 18.76236 -2.135498 -2.333342

72 22.1914 19.77444 19.57381 -2.41696 -2.617592

73 23.3631 20.87877 20.59973 -2.484335 -2.763372

74 24.6147 21.99571 21.71285 -2.618988 -2.901854

75 25.9501 23.11266 22.82597 -2.837442 -3.124132

76 27.3953 24.3189 23.93909 -3.076405 -3.456211

77 28.9943 25.97165 25.53612 -3.022654 -3.458179

78 30.8531 27.6244 27.18321 -3.228699 -3.669886

79 33.1577 29.27714 28.83031 -3.880558 -4.327393

　と、なり、360 / 365.25度にせよ、360 / 364度（なぜ、この数値も考慮したかは、第３節で詳説する予定である）にせよ、計算値としては、いささか数値が合わない結果となった。『宣明暦』における二十四節気の影の長さの正確さと比べて、差が大きいようである。したがって、我々は、インド伝来という説を採ることができない。

３　華度とTAN表の制作方法。

　ここで、視点を変えて、もし、『宣明暦』の表に誤差が全く無いものだったら、と仮定してみよう。もちろん、TAN表が一部分でも３次方程式になっているわけではないから、勿論、誤差は避けられないのだが、敢えてこの仮定で考えてみる。つまり、従来の研究では、１華度を360/365.25として誤差を計算していたのに対し、華度の部分を変えることはできないかと考えたのである。そこで、反対に、この表の値から、１華度が何度になるかを計算したのが、先ほどの表１の３行目である。１華度が、360 / x　度になっているかを示している。　先に述べたように、値が前後するのは、記述の構造上仕方がないが、ここで、常識的に考えられた 360 / 365.25　とは、かなり隔たりがあることが分かる。

さらに、１華度を360/363度から360/366度まで分母を0.01華度ずつ変化させたときに誤差の絶対値の総和を計算したものを図にしたものが、図１である。系列１は、81”度”すべてについて、また、系列２は、劉金沂・趙澄秋も指摘しているように正確と思われる60華度以下の部分について、作図したものである。

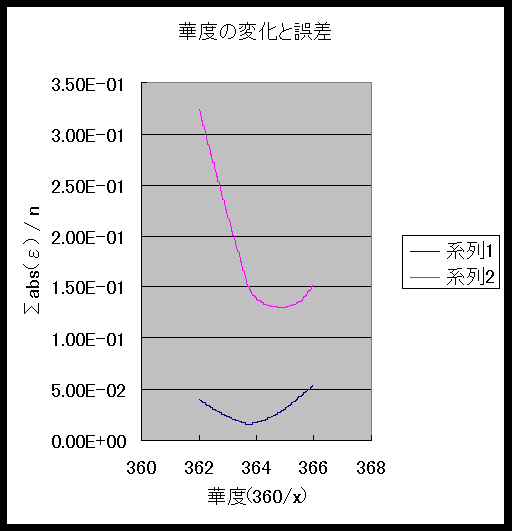
これを見る限り、１華度＝360 / 364　付近が一番誤差が少ないことを示している。　365.25（日）という数値は、言うまでもなく１回帰年の日数である。一行の『大衍暦』では、１朔望月との比率を整えるために、本来の測定値より敢えて長めになっているが、それでも、365.2444日である。したがって、364という数値は、天文学的な数値としては考えられないものである。

　しかし、『新唐書』には、次のような記述があり、１象限を概数として９１度とすることも行われていた可能性はある。

　すなわち、『新唐書』巻二十七下 志第十七下 暦三下には、

とあり、９１華度が１象とあるからである。

いずれにせよ、364という数値は、１象限を９１等分したということは論を待たない。

　と、いう事は、模型を作ったと考えるのが自然ではないだろうか。それならば、その模型で、TANの値を実測したと考えるのは不可能であろうか。

　『隋書』「律暦志」の記載によれば、

とあり、直径１丈、すなわち、半径５尺の大きな円を作ったという記述である。このような円を使って９１等分するのも不可能とばかりは、言えないのではないだろうか。熟練者ならTAN表の数値を相当の精度で測定しうる可能性がありそうである。

４　まとめ　以上の考察から、世界最初のTAN表では、１華度＝360/364度を使っていた可能性は強そうである。本来、360/（１回帰年の日数）であるべき数値であるが、これを変えたということは、注意しなければならない。模型を作って、実測するためではないかという第３節で述べた仮説と共に、天上界と地上界とを違う基準にしたとすれば、近代科学との比較にも注意すべきであろう。

　中国では、古から「天円地方」というように、形状の違いは認めていた。しかし、更に、数値を天と地で変える、あるいは、地上を基準として、天をあるがままではなく、捉えやすいように基準を変えて捉えるということだとしたら、これは思想上にも大きな問題となるのではないだろうか。

また、『宣明暦』は、日本では、800年以上も使われた暦である。この原因は色々あるのだろうが、緯度が異なっても、基本となる実測値が得やすいということも影響したのではないだろうか。中国以外の諸国でも、太陽の南中高度が分かれば、基本定数が計算できるのであれば、各国でも応用しやすいと考えられる。一年に一度の夏至や冬至の測定は、天候によって、できないときも多い。

写真４、北京古観象台の８尺の表による実測の図

写真５、北京古観象台の８尺の表

影の長さを測るより、高度を測った方が誤差も少なくなり、重宝だったのではないだろうか。また、天候により太陽を測定できないことも多いはずである。その日が夏至とか重要な節気の時は、大変である。しかし、前後数日の測定から、計算することも不可能ではない。

緯度（北緯）φにおける太陽の南中高度hは、緯度φ、春分点からの角度x、赤道と黄道の交差角εとすると、

h＝90 -φ＋sin'(sinε・sin ｘ)

となる。これは、高さｂの「表」を立てた影の長さｙ

ｙ＝ｂ・cot h

＝ｂ・tan 〔φ - sin'(sinε・sin ｘ) 〕

と比べて、tanの計算がない分だけ、計算が簡単になる。

　階差をとって複雑な関数を分析するという中国数学の伝統的方法を使い、前後数日の太陽の南中高度から、求める日の南中高度を計算することも可能だろう。

参考文献

銭宝「玉宗」. 1964.『中国数学史』、北京:科学出版社.

Cullen, Christopher. 1982. "An Eighth Century Chinese Table of Tangent". Chinese Science, 1982,5: 1 -33.

中外数学簡史編写組（編）、1987.『外国数学簡史』、済南:山東教育出版社.

劉金沂・趙澄秋. 1986. "唐代一行編成世界最早的正接函数表". 自然科学史研究 vol.5 No.4 (1986):298-309.

中国天文学史整理研究小組（編）、1987、『中国天文学史』、北京:　科学出版社。

城地　茂.1989."祖沖之の 『大明暦』 と円周率の計算". 北京師範大学学報（自然科学版）1989-4: 85-9.

城地　茂.1990. 「中国の圭表の一考察 -清代10尺の圭表の 2つの仮説」.数学史研究 124: 10-15.

林隆夫、1993、『インドの数学』、東京:中央公論社（中公新書1155）

曲安京. 1997. 「一行の正接関数表（７２４年）」. 数学史研究, 153: 18 - 29.

原典の版本

『二十五史』全12冊、上海古籍出版社・上海書店、1986.『開元占経』、瞿曇悉達、北京：中国書店、1989.

『高麗史』、鄭麟趾、台北：文史哲出版、1972.

任継愈、『中国科学技術典籍通彙』「数学巻」全５巻、河南教育出版社、1993.