「プラトーの問題」というのは，数学的な「極小曲面」の問題のこと。

極小曲面とは？

空間内にに与えられた一つの閉曲線で囲まれた曲面のうち面積最小のものを「極小曲面」と言う。 極小曲面の上ではどこでも平均曲率が０である。すなわち，曲面上の任意の点Ｏにおいて互いに直交する，曲面に沿う２本の曲線を考えると（図中の曲線ＡＯＢとＣＯＤ），それ らの曲率は等しく，曲率中心は曲面に対して互いに反対側にある。

　シャボン玉の丸い形や，枠に張られたシャボン膜の形。このおもしろさは，昔の物理学者たちの関心をさそった。それらの形は，液体の表面積が最小になろうとする傾向のあらわれであり，これから表面張力の概念が導かれたとも言える。

　どうしてあのような膜ができるのかというのは，ここで紹介しているように ，表面張力によってできるだけ膜の表面積が小さくて済むような形になるからなのです。

　歴史を振り返ってみると，1873年プラトーが「空間内に与えられた一つの閉曲線で囲まれた曲面のうち面積最小のものを見 出せ」という最小問題をシャボン膜を使って解いている。そこから，この問題のことをプラトーの問題と呼ぶ訳なのです。

つまり，プラトーは枠に張られたシャボン膜が極小曲面であることを発見したのです。正確に言うと，プラトーは，液体は重力の影響 を受けずに自由な形をとらせるならば，最小の面積をとることを実証的に証明した最初の人物だったのです。

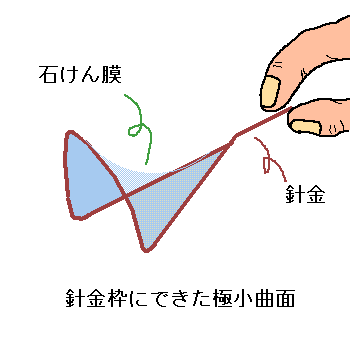右図もその最小曲面を示した一つです。その内容は，主曲率半径がＬおよびＲであるような曲面では常に，

が成立するような面をシャボン膜が作ることを示した。幾何学によれば，この条件があてはまるときに表面は最小面積をとるからである。

さらに，プラトーは重力の影響を除いた面を作るのにシャボン膜を用いたほか， オリーブ油をそれと同じ比重にした水とアルコールの混合液に加えて，完全に丸 い油の球を作って見せた。この場合も，針金の枠を用いて，いろいろな曲面を作ることができたのです。

はじめに戻る

参考文献